MPC Protocols
MPC Protocols
MPC protocols differ based on their security models, cryptographic assumptions, and efficiency. In terms of security models, we have:
Honest but Curious: All participants behave according to the protocol while trying to gather as much information as possible from the exchanged data.
Honest Majority: Require at least N/2 participants to act honestly, ensuring data privacy and integrity.
Dishonest Majority: Can withstand up to N-1 participants acting maliciously, still guaranteeing privacy and correctness, as long as one participant remains honest.
MPC protocols can be further categorized by their cryptographic assumptions:
Computationally Secure: Relies on the difficulty of mathematical problems (e.g., factoring large numbers). These systems are generally secure today but may be vulnerable in the future, especially with the advent of quantum computing.
Information-Theoretically Secure: Achieves security based on principles of information theory, without relying on computational hardness (e.g., Additive Secret Sharing). These are more robust but tend to be less efficient.
State-of-the-art MPC protocols, including those in the Arcium Network, typically adopt a preprocessing model, where the most expensive cryptographic operations are conducted in advance in an offline phase. The online phase then executes the actual computation efficiently using the precomputed values.
Both of these systems rely on the use of secret sharing, i.e. splitting up a value and providing a share to each participant. The properties of these shares allow the addition of two shares and multiplication by a constant to be performed locally by each peer. Share multiplication requires some communication between peers. To verify the soundness of a value when it is sent from one peer to another, these schemes rely on MACs (Message-Associated Codes) which peers cannot forge. These MACs help guarantee that no cheating has occurred: if forgery is spotted, a peer can choose to unilaterally abort the protocol.
Oblivious transfer-based protocols: OT is a simple but powerful cryptographic primitive that allows a sender to send two messages A and B to a receiver, who can then learn either A or B, while not letting the sender know which one he picked. These protocols can typically be made computationally efficient but involve heavy communication overhead between players, though recent advances in silent OT protocols have made these methods significantly more competitive.
FHE and ZKP-based methods: these protocols combine Fully Homomorphic Encryption (FHE) and Zero-Knowledge Proofs (ZKPs) to pass around messages between peers in an encrypted manner and compute on them as needed to produce valid preprocessing values. The ZKPs are typically used to verify the correctness of the FHE ciphertexts, ensuring peers cannot maliciously deviate from the protocol without being detected. These protocols are rather efficient in terms of their communication overhead, but the computations involved for FHE remain fairly heavy despite recent advances.
MPC Vs. Other Encryption Techniques
Encrypted Computation is essential for enabling privacy in a range of digital ecosystems, including blockchain-integrated applications.
While various solutions exist, they are not all equally suited to meet the diverse demands of decentralized and hybrid on-chain/off-chain applications.
Here's how different techniques compare.
Fully Homomorphic Encryption (FHE)
FHE allows computations on encrypted data without needing decryption, which ensures data privacy throughout the process. Although it has been touted as a future-proof encryption method, FHE suffers from high computational costs, which currently limit its transaction processing speed to around 5 TPS. Despite recent advances, large-scale blockchain implementations remain impractical. FHE also relies on specific decryption processes that could be exploited if not securely managed, posing scalability and performance challenges.
Trusted Execution Environments (TEEs)
TEEs enable private computation by running tasks within a secure, isolated area of a device's hardware. Although already in production and capable of high performance, TEEs have proven vulnerable to side-channel attacks, where attackers deduce confidential information by monitoring specific hardware behaviors. This need for trusted hardware providers also poses a security risk, as breaches could compromise the whole environment. In contrast, cryptographic solutions like MPC do not require hardware-specific trust, offering a more flexible approach to secure computations.
Zero-Knowledge Proofs (ZKPs)
ZKPs allow one party to prove the accuracy of a statement without revealing the underlying data. This makes them highly effective for verifying off-chain computations. However, ZKPs fall short in shared state systems like blockchains, where multiple parties need to interact simultaneously with the same encrypted data. They are better suited for niche use cases, such as selective disclosure, rather than comprehensive on-chain encryption.
Secure Multi-Party Computation (MPC): The Optimal Solution
MPC has emerged as the most versatile and scalable method for decentralized confidentiality. It allows multiple parties to compute a function collaboratively, ensuring that each party's data remains private. MPC is faster and more cost-effective than FHE, making it more suitable for real-time applications. TEEs provide faster execution but relies on trusted hardware that can be exploited and fails to provide a truly trustless solution. MPC protocols also offer robust security: the computation's result is guaranteed to be correct even if a subset of participants behaves maliciously.
MPC stands out for its:
High Security: Supports trustless, decentralized execution without relying on specific hardware or intermediaries.
Flexibility: Suitable for a range of use cases across Web3, from AI to DeFi.
Cost and Speed Efficiency: Outperforms other encryption techniques like FHE in terms of operational efficiency. With advancements from platforms like Arcium, MPC can now be deployed at scale, unlocking countless high-value on-chain applications. Other methods like FHE, TEEs, and ZKPs have their merits but fail to offer the same blend of security, flexibility, and performance needed for comprehensive on-chain encryption.
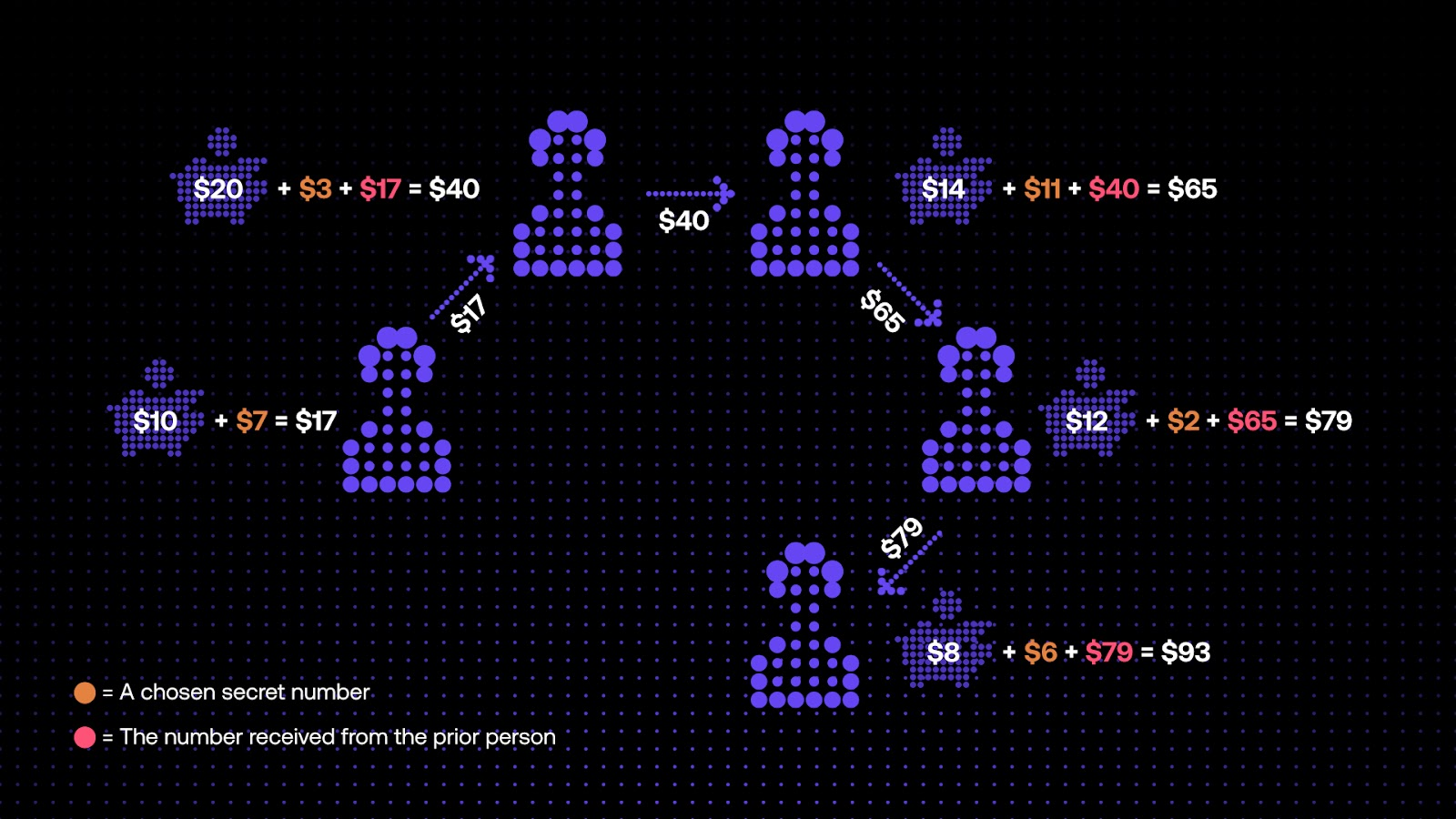
MPC at Arcium
Arcium's engineers are working on deploying two different MPC backends, nicknamed Cerberus and Manticore. These two backends make different tradeoffs and enable a wider range of applications.
Cerberus is the main backend for MPC computations. Each share is authenticated with a MAC and honest nodes can identify malicious behavior and abort the computation. Under the assumption that at least one node is honest, this means that the computation's result is guaranteed to be correct. Cerberus provides the strongest security guarantees.
Manticore operates in the honest but curious setting. It also relies on a Trusted Dealer, a node that generates the preprocessing data needed for the online phase and then goes offline. This leads to faster execution time that allows more complex operations typical of machine learning/AI applications. However, the security guarantees are weaker. Manticore is meant to be deployed in settings where the nodes are trusted operators and have an incentive to behave honestly.
As an example, it would be possible to train a machine learning model using Manticore since it is a computationally intensive task. It would then be possible to use Cerberus to make predictions using this newly trained model.
Last updated
